呼び出しでつながる複数のメソッド

高校の数学で習った階乗と順列・組合せを思い出してください。

階乗

特に、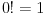と定める。

順列の総数

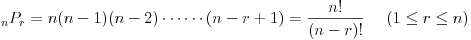
特に、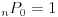と定める。

組合せの総数

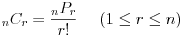
特に、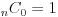と定める。

今回は、これらの値を計算する3つのメソッドを作ることが目的となります。 順列の総数は階乗を使って求められ、組合せの総数は階乗と順列の総数を使って求められることに注意してください。

このことから、3つのメソッドを次のように作っていけばよいでしょう。

• factorialメソッド: 階乗を計算するメソッド。他のメソッドで呼び出される。
• permutationメソッド: 順列を計算するメソッド。内部でfactorialメソッドを呼び出す。
• combinationメソッド: 組合せを計算するメソッド。内部でfactorialメソッドとpermutationメソッドを呼び出す。

factorialメソッドという一番小さな部品から、permutationメソッドやcombinationメソッドという大きな部品を作り上げていく感覚になります。

階乗を求めるメソッドを用意する

まずは、factorialメソッドを作って動作を確かめてみましょう。 MethodSample06は、0!から20!までを計算して表示するプログラムです。

MethodSample06.java

class MethodSample06 {
    /*---- 階乗を求める ----*/
    static int factorial(int n){
        int factorial = 1;
        for(int i = 2; i <= n; i++){
            factorial *= i;
        }
        return factorial;
    }

    public static void main(String[] args) {
        for(int i = 0; i <= 20; i++){
            int f = factorial(i);
            System.out.println(i + "! = " + f);
        }
    }
}

MethodSample06の実行結果

0! = 1
1! = 1
2! = 2
3! = 6
4! = 24
    （中略）
11! = 39916800
12! = 479001600
13! = 1932053504
14! = 1278945280
    （中略）
20! = -2102132736

factorialメソッドの処理内容はシンプルですが、解説すべき点が意外にたくさんあります。

まず、factorialというローカル変数が宣言されていますね。 これはメソッド名と同じですが、問題はありません。 メソッドと変数は種類が異なるものなので、名前が衝突しないからです。

次に、factorialメソッドのfor文の初期化部を見てください。 「int i = 2」となっています。 このため、仮引数nの値が0か1のときは、ループ本体が一回も実行されず、変数factorialの初期値1が、そのまま戻り値として返されます。 仮引数nが2以上なら、ループ本体が少なくとも一回は実行され、変数factorialに2, 3, 4, ..., nが次々にかけられていきます。 このようにして、変数factorialには最終的にn!が格納されることになります。

また、実行結果をよく見ると、おかしな点に気づかれるでしょう。 12! = 479001600は正しいのですが、13! = 1932053504は間違いで、正しくは13! = 6227020800です。 実は、13!以降はすべて間違いなのです。 中にはマイナスの値も含まれていますね。 正の整数をかけ合わせたのに、そんな結果になるはずがありません。 これはint型の変数が最大で2147483647までしか表せないことが原因です。 ともあれ、0!から12!までは正確に計算することができます。

階乗を求めるメソッドの活用

それではいよいよ、factorialメソッドを応用して、permutationメソッドとcombinationメソッドを作ってみましょう。 MethodSample07は、キーボードから整数nとrを入力して、nPrとnCrをそれぞれ計算し、結果を表示するプログラムです。 キーボード入力では、nは0以上12以下、rは0以上n以下の値だけを受け付け、それ以外は再入力を促します。

MethodSample07.java

import java.io.*;

class MethodSample07 {
    /*---- 階乗を求める ----*/
    static int factorial(int n){
        int factorial = 1;
        for(int i = 2; i <= n; i++){
            factorial *= i;
        }
        return factorial;
    }

    /*---- 順列の総数を求める ----*/
    static int permutation(int n, int r){
        int p = factorial(n) / factorial(n - r);
        return p;
    }

    /*---- 組合せの総数を求める ----*/
    static int combination(int n, int r){
        int c = permutation(n, r) / factorial(r);
        return c;
    }

    public static void main(String[] args) throws IOException{
        BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
        int n, r;

        do{
            System.out.print("0以上12以下の整数n： ");
            n = Integer.parseInt(br.readLine());
        }while(n < 0 || 12 < n);
        do{
            System.out.print("0以上" + n + "以下の整数r： ");
            r = Integer.parseInt(br.readLine());
        }while(r < 0 || n < r);
        System.out.println(n + " P " + r + " = " + permutation(n, r));
        System.out.println(n + " C " + r + " = " + combination(n, r));
    }
}

MethodSample07の実行結果 1

0以上12以下の整数n： 5
0以上5以下の整数r： 2
5 P 2 = 20
5 C 2 = 10

MethodSample07の実行結果 2

0以上12以下の整数n： 6
0以上6以下の整数r： 0
6 P 0 = 1
6 C 0 = 1

MethodSample07の実行結果 3

0以上12以下の整数n： 7
0以上7以下の整数r： 7
7 P 7 = 5040
7 C 7 = 1

permutationメソッドとcombinationメソッドは、次のようになっています。

    /*---- 順列の総数を求める ----*/
    static int permutation(int n, int r){
        int p = factorial(n) / factorial(n - r);
        return p;
    }

    /*---- 組合せの総数を求める ----*/
    static int combination(int n, int r){
        int c = permutation(n, r) / factorial(r);
        return c;
    }

どちらのメソッドも、数学的な式をJava言語で書き表しただけの簡潔な内容です。 combinationメソッドでは、permutationメソッドとfactorialメソッドを呼び出しています。 そして、permutationメソッドからは、更にfactorialメソッドを呼び出しています。

既存のメソッドを活用して、新しいメソッドを組み立てることができる。