受け取った多次元配列の内容を変更する

MethodSample12は2つの行列の和を求めるプログラムです。

MethodSample12.java

class MethodSample12 {
    /*---- 行列xとyの和をzに代入する ----*/
    static void addMatrix(int[][] x, int[][] y, int[][] z){
        for(int i = 0; i < x.length; i++)
            for(int j = 0; j < x[i].length; j++)
                z[i][j] = x[i][j] + y[i][j];
    }

    /*---- 行列mの内容を表示する ----*/
    static void printMatrix(int[][] m){
        for(int i = 0; i < m.length; i++){
            for(int j = 0; j < m[i].length; j++)
                System.out.printf(" %2d", m[i][j]);
            System.out.println();
        }
    }

    public static void main(String[] args){
        int[][] a = { {1, 0, 1}, {0, -4, 2} };
        int[][] b = { {5, -3, 0}, {0, 2, -1} };
        int[][] c = new int[2][3];

        addMatrix(a, b, c);

        System.out.println("行列a");    printMatrix(a);
        System.out.println();
        System.out.println("行列b");    printMatrix(b);
        System.out.println();
        System.out.println("行列c");    printMatrix(c);
    }
}

ここでは、予め用意された2行3列の行列の和を求めています。

実際に行列の和を求めるのはaddMatrixメソッドです。 このメソッドは、行列を表す2次元配列xとyを受け取り、その和を2次元配列zに代入します。

    /*---- 行列xとyの和をzに代入する ----*/
    static void addMatrix(int[][] x, int[][] y, int[][] z){
        for(int i = 0; i < x.length; i++)
            for(int j = 0; j < x[i].length; j++)
                z[i][j] = x[i][j] + y[i][j];
    }

addMatrixメソッドは、行列x, y, zの行数と列数が完全に一致していることを前提としています。 例えば、x[0]の長さよりz[0]の長さが短い場合、実行時にエラーとなります。

二重のfor文で行列の和を求める様子を示すのが、図 9-12です。

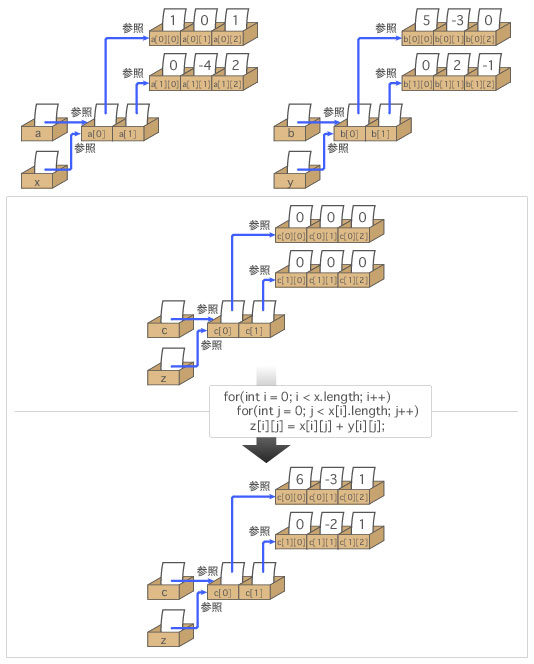
MethodSample12では、2次元配列の内容を表示する回数が多いので、表示専用のprintMatrixメソッドに配列の表示をすべて任せています。

    /*---- 行列mの内容を表示する ----*/
    static void printMatrix(int[][] m){
        for(int i = 0; i < m.length; i++){
            for(int j = 0; j < m[i].length; j++)
                System.out.printf(" %2d", m[i][j]);
            System.out.println();
        }
    }

多次元配列を返す

メソッドは多次元配列を返すこともできます。 MethodSample12のaddMatrixは、引数として受け取ったzに和を代入していましたが、和を戻り値として返すように作り替えることもできるのです。 ここでは、敢えて別のプログラムを扱ってみます。

MethodSample13は行列の整数倍を求めるプログラムです。

MethodSample13.java

class MethodSample13 {
    /*---- 行列xのk倍を返す ----*/
    static int[][] multiplyMatrixByScalar(int[][] x, int k){
        int[][] y = new int[x.length][];
        for(int i = 0; i < x.length; i++){
            y[i] = new int[x[i].length];
            for(int j = 0; j < x[i].length; j++)
                y[i][j] = k * x[i][j];
        }
        return y;
    }

    /*---- 行列mの内容を表示する ----*/
    static void printMatrix(int[][] m){
        for(int i = 0; i < m.length; i++){
            for(int j = 0; j < m[i].length; j++)
                System.out.printf(" %2d", m[i][j]);
            System.out.println();
        }
    }

    public static void main(String[] args){
        int[][] a = { {1, -2, 0}, {0, -1, 3} };

        int[][] b = multiplyMatrixByScalar(a, 2);

        System.out.println("行列a");    printMatrix(a);
        System.out.println();
        System.out.println("行列b");    printMatrix(b);
    }
}

ここでは、予め用意された2行3列の行列の2倍を求めています。

実際に行列を整数倍するのはmultiplyMatrixByScalarメソッドです。 このメソッドは、行列を表す2次元配列xと整数kを受け取り、xの各要素をk倍して得られた2次元配列を返します。

    /*---- 行列xのk倍を返す ----*/
    static int[][] multiplyMatrixByScalar(int[][] x, int k){
        int[][] y = new int[x.length][];
        for(int i = 0; i < x.length; i++){
            y[i] = new int[x[i].length];
            for(int j = 0; j < x[i].length; j++)
                y[i][j] = k * x[i][j];
        }
        return y;
    }

multiplyMatrixByScalarメッソドで、行列の整数倍を求める様子を示すのが、図 9-14です。

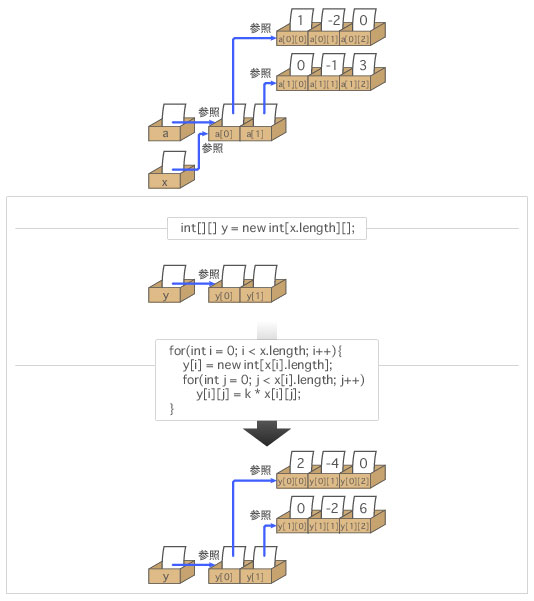
MethodSample12と同様、行列の表示はprintMatrixメソッドに任せています。